▣ 문제
오늘은 새 학기 새로운 반에서 처음 시작하는 날이다. 현수네 반 학생은 N명이다. 현수는 각 학생들의 친구관계를 알고 싶다. 모든 학생은 1부터 N까지 번호가 부여되어 있고, 현수에게는 각각 두 명의 학생은 친구 관계 가 번호로 표현된 숫자쌍이 주어진다. 만약 (1, 2), (2, 3), (3, 4)의 숫자쌍이 주어지면 1번 학 생과 2번 학생이 친구이고, 2번 학생과 3번 학생이 친구, 3번 학생과 4번 학생이 친구이다. 그리고 1번 학생과 4번 학생은 2번과 3번을 통해서 친구관계가 된다. 학생의 친구관계를 나타내는 숫자쌍이 주어지면 특정 두 명이 친구인지를 판별하는 프로그램 을 작성하세요. 두 학생이 친구이면 “YES"이고, 아니면 ”NO"를 출력한다.
▣ 입력설명
- 첫 번째 줄에 반 학생수인 자연수 N(1<=N<=1,000)과 숫자쌍의 개수인 M(1<=M<=3,000)이 주어지고, 다음 M개의 줄에 걸쳐 숫자쌍이 주어진다. 마지막 줄에는 두 학생이 친구인지 확인하는 숫자쌍이 주어진다.
▣ 출력설명
- 첫 번째 줄에 “YES"또는 "NO"를 출력한다.
▣ 입력 예시
| 9 7 1 2 2 3 3 4 4 5 6 7 7 8 8 9 3 8 |
▣ 출력 예시
| NO |
<코드>
#pragma warning(disable:4996)
#include<stdio.h>
int unf[1001];
int Find(int v) {
if (v == unf[v]) return v;
else return Find(unf[v]);
}
void Union(int a, int b) {
a = Find(a);
b = Find(b);
if (a != b) unf[a] = b;
}
int main() {
int i, n, m, a, b, fa, fb;
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++) {
unf[i] = i;
}
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
Union(a, b);
}
scanf("%d %d", &a, &b);
fa = Find(a);
fb = Find(b);
if (fa == fb) printf("YES\n");
else printf("NO\n");
return 0;
}Union&Find 자료구조는 Disjoint-Set, 서로소인 집합,을 표현할때 쓰는 알고리즘이다. 즉, 두 집합간 공통 원소가 존재하지 않는다.
이를 구현하는데 트리 구조를 이용한다.
우선 트리 구조를 구현하기 위해서 1차원 배열인 unf[1001]을 만든다. unf[1001] 배열의 인덱스(Index)는 학생을 표현하고 값은 부모 노드의 번호를 표현한다.
입력 예시를 예로 들면,
Union(1,2) 에서 a = Find(1) = 1, b = Find(2) = 2 이기 때문에
unf[1] = 2 가 된다. 즉, 처음 자기 번호로 표현된 unf[ ] 배열이 다음과 같이 변한다.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| unf[i] | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Union(2,3), Union(3,4) 에 똑같이 적용하면,
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| unf[i] | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 |

다음 Union(1,5)를 보면 a = Find(1) = Find(2) = Find(3) = Find(4) = 4
b = Find(5) = 5
가 되고 결과적으로 unf[4] = 5 가 된다.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| unf[i] | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 | 9 |

그 뒤로 Union(6,7), Union(7,8), Union(8,9)의 결과를 보면
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| unf[i] | 2 | 3 | 4 | 5 | 5 | 7 | 8 | 9 | 9 |

와 같이 된다.
마지막으로 fa와 fb라는 노드의 부모 노드가 같으면 서로 연결되어있다고 판단할 수 있다.
이처럼 Find 함수는 재귀를 반복하기 때문에 시간 복잡도가 O(N)이다. 이를 최적화 시킬수 있는 방법으로 '경로 압축'이라는 방법을 쓸 수 있다.
#pragma warning(disable:4996)
#include<stdio.h>
int unf[1001];
int Find(int v) {
if (v == unf[v]) return v;
else return unf[v] = Find(unf[v]);
}
void Union(int a, int b) {
a = Find(a);
b = Find(b);
if (a != b) unf[a] = b;
}
int main() {
int i, n, m, a, b, fa, fb;
scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++) {
unf[i] = i;
}
for (i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
Union(a, b);
}
scanf("%d %d", &a, &b);
fa = Find(a);
fb = Find(b);
if (fa == fb) printf("YES\n");
else printf("NO\n");
return 0;
}코드를 보게되면 Find 함수에
else return unf[v] = Find(unf[v]);
로 수정이 되었다.
이 코드의 흐름을 살펴보자면
Union(1,2), Union(2,3), Union(3,4)는 동일하게 움직인다.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| unf[i] | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 |

여기서 Union(1,5)는 a = Find(1)
= unf[1] = Find(2)
= unf[2] = Find(3)
= unf[3] = Find(4) = 4
b = Find(5) = 5
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| unf[i] | 4 | 4 | 4 | 5 | 5 | 6 | 7 | 8 | 9 |
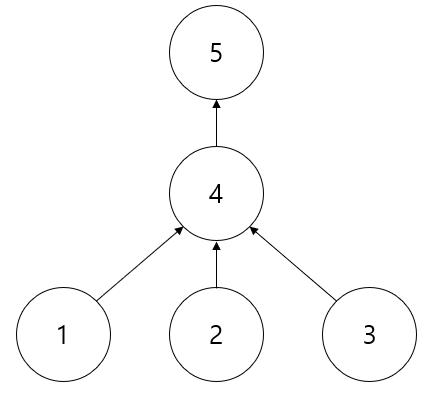
보이는것처럼 트리의 레벨이 이전보다 줄어들었기 때문에 시간복잡도가 O(logN)으로 줄어든다.
'[c언어&c++] 알고리즘 공부 > 개념' 카테고리의 다른 글
| [개념] 네트워크 선 자르기(Bottom-Up, DP) / c++ & c / 제한시간 없음 (0) | 2021.02.27 |
|---|---|
| [개념] 조합 구하기 / c & c++ / 제한시간 없음 (0) | 2021.02.22 |
| [개념] 이항계수(메모이제이션) / c & c++ / 제한시간 없음 (0) | 2021.02.18 |
| [개념] 최대힙(priority_queue, 우선순위큐) / c++ / 제한시간 없음 (0) | 2021.02.17 |
| [개념] 최소비용(DFS, 가중치 방향그래프 인접리스트,STL pair)/ c++ / 제한시간 없음 (0) | 2021.02.17 |